Odds are a mathematical way of explaining how likely or unlikely something is to happen. You can use odds in two different formats. The first one is a percentage and the second is a ratio. Some players find percentages easier to work with, but you need to learn how to consider Texas holdem odds as ratios. The probability of the turn card being a heart is then 9/47 &asymp 0.19. The probability of the turn card notbeing a heart but getting a heart on the river is (38/47) (9/46) &asymp 0.16. Therefore the total probability of getting a flush is approximately 0.19 + 0.16 = 0.35.

The main underpinning of poker is math – it is essential. For every decision you make, while factors such as psychology have a part to play, math is the key element.

For example, whenever you hold four cards to a nut flush on the turn in a Texas Hold’em game, there are 46 unknown cards, (52 minus your two pocket cards and four on the board). Of those 46 cards, 37 cards won’t help you, but those other nine cards are the same suit as your flush draw and any one of them will give you the nut flush. For example: To calculate your hand odds in a Texas Hold'em game when you hold two hearts and there are two hearts on the flop, your hand odds for making a flush are about 2 to 1. This means that for approximately every 3 times you play this hand, you can expect to hit your flush one of those times.

In this lesson we’re going to give an overview of probability and how it relates to poker. This will include the probability of being dealt certain hands and how often they’re likely to win. We’ll also cover how to calculating your odds and outs, in addition to introducing you to the concept of pot odds. And finally we’ll take a look at how an understanding of the math will help you to remain emotional stable at the poker table and why you should focus on decisions, not results.

What is Probability?

Probability is the branch of mathematics that deals with the likelihood that one outcome or another will occur. For instance, a coin flip has two possible outcomes: heads or tails. The probability that a flipped coin will land heads is 50% (one outcome out of the two); the same goes for tails.

Probability and Cards

When dealing with a deck of cards the number of possible outcomes is clearly much greater than the coin example. Each poker deck has fifty-two cards, each designated by one of four suits (clubs, diamonds, hearts and spades) and one of thirteen ranks (the numbers two through ten, Jack, Queen, King, and Ace). Therefore, the odds of getting any Ace as your first card are 1 in 13 (7.7%), while the odds of getting any spade as your first card are 1 in 4 (25%).

Unlike coins, cards are said to have “memory”: every card dealt changes the makeup of the deck. For example, if you receive an Ace as your first card, only three other Aces are left among the remaining fifty-one cards. Therefore, the odds of receiving another Ace are 3 in 51 (5.9%), much less than the odds were before you received the first Ace.

Want to see how poker math intertwines with psychology and strategy to give you a MASSIVE EDGE at the tables? Check out CORE and learn poker in the quickest and most systematic way:

Pre-flop Probabilities: Pocket Pairs

In order to find the odds of getting dealt a pair of Aces, we multiply the probabilities of receiving each card:

(4/52) x (3/51) = (12/2652) = (1/221) ≈ 0.45%.

To put this in perspective, if you’re playing poker at your local casino and are dealt 30 hands per hour, you can expect to receive pocket Aces an average of once every 7.5 hours.

The odds of receiving any of the thirteen possible pocket pairs (twos up to Aces) is:

(13/221) = (1/17) ≈ 5.9%.

In contrast, you can expect to receive any pocket pair once every 35 minutes on average.

Pre-Flop Probabilities: Hand vs. Hand

Players don’t play poker in a vacuum; each player’s hand must measure up against his opponent’s, especially if a player goes all-in before the flop.

Here are some sample probabilities for most pre-flop situations:

Post-Flop Probabilities: Improving Your Hand

Now let’s look at the chances of certain events occurring when playing certain starting hands. The following table lists some interesting and valuable hold’em math:

Many beginners to poker overvalue certain starting hands, such as suited cards. As you can see, suited cards don’t make flushes very often. Likewise, pairs only make a set on the flop 12% of the time, which is why small pairs are not always profitable.

PDF Chart

We have created a poker math and probability PDF chart (link opens in a new window) which lists a variety of probabilities and odds for many of the common events in Texas hold ‘em. This chart includes the two tables above in addition to various starting hand probabilities and common pre-flop match-ups. You’ll need to have Adobe Acrobat installed to be able to view the chart, but this is freely installed on most computers by default. We recommend you print the chart and use it as a source of reference.

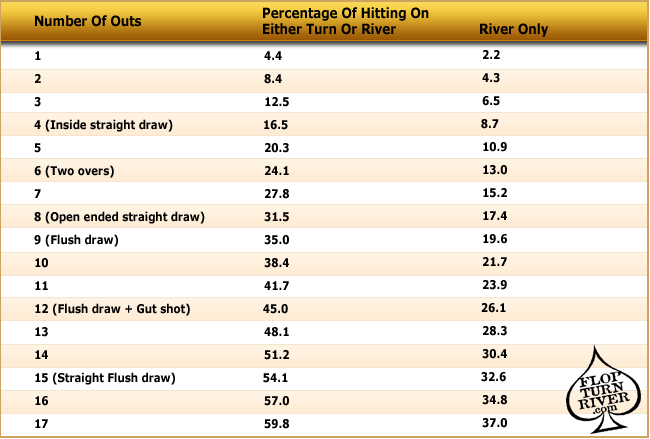
Odds and Outs

If you do see a flop, you will also need to know what the odds are of either you or your opponent improving a hand. In poker terminology, an “out” is any card that will improve a player’s hand after the flop.

One common occurrence is when a player holds two suited cards and two cards of the same suit appear on the flop. The player has four cards to a flush and needs one of the remaining nine cards of that suit to complete the hand. In the case of a “four-flush”, the player has nine “outs” to make his flush.

A useful shortcut to calculating the odds of completing a hand from a number of outs is the “rule of four and two”. The player counts the number of cards that will improve his hand, and then multiplies that number by four to calculate his probability of catching that card on either the turn or the river. If the player misses his draw on the turn, he multiplies his outs by two to find his probability of filling his hand on the river.

In the example of the four-flush, the player’s probability of filling the flush is approximately 36% after the flop (9 outs x 4) and 18% after the turn (9 outs x 2).

Pot Odds

Another important concept in calculating odds and probabilities is pot odds. Pot odds are the proportion of the next bet in relation to the size of the pot.

For instance, if the pot is $90 and the player must call a $10 bet to continue playing the hand, he is getting 9 to 1 (90 to 10) pot odds. If he calls, the new pot is now $100 and his $10 call makes up 10% of the new pot.

Experienced players compare the pot odds to the odds of improving their hand. If the pot odds are higher than the odds of improving the hand, the expert player will call the bet; if not, the player will fold. This calculation ties into the concept of expected value, which we will explore in a later lesson.

Bad Beats

A “bad beat” happens when a player completes a hand that started out with a very low probability of success. Experts in probability understand the idea that, just because an event is highly unlikely, the low likelihood does not make it completely impossible.

A measure of a player’s experience and maturity is how he handles bad beats. In fact, many experienced poker players subscribe to the idea that bad beats are the reason that many inferior players stay in the game. Bad poker players often mistake their good fortune for skill and continue to make the same mistakes, which the more capable players use against them.

Decisions, Not Results

One of the most important reasons that novice players should understand how probability functions at the poker table is so that they can make the best decisions during a hand. While fluctuations in probability (luck) will happen from hand to hand, the best poker players understand that skill, discipline and patience are the keys to success at the tables.

A big part of strong decision making is understanding how often you should be betting, raising, and applying pressure.
The good news is that there is a simple system, with powerful shortcuts & rules, that you can begin using this week. Rooted in GTO, but simplified so that you can implement it at the tables, The One Percent gives you the ultimate gameplan.

This 7+ hour course gives you applicable rules for continuation betting, barreling, raising, and easy ratios so that you ALWAYS have the right number of bluffing combos. Take the guesswork out of your strategy, and begin playing like the top-1%.

Conclusion

A strong knowledge of poker math and probabilities will help you adjust your strategies and tactics during the game, as well as giving you reasonable expectations of potential outcomes and the emotional stability to keep playing intelligent, aggressive poker.

Remember that the foundation upon which to build an imposing knowledge of hold’em starts and ends with the math. I’ll end this lesson by simply saying…. the math is essential.

By Gerald Hanks

Gerald Hanks is from Houston Texas, and has been playing poker since 2002. He has played cash games and no-limit hold’em tournaments at live venues all over the United States.

Mathematics: Flushes & Straights : Simple Pot Odds : Implied Odds : Reverse Implied Odds

Watch SplitSuit's video on Flushes and Flush Draws for 8 hand histories involving strategy on playing flushes in Texas Hold'em.

You are on the flop with a pretty decent flush draw. You have two hearts in your hand and there are another two on the flop.

Unfortunately, some cool cat has made a bet, putting you in a tricky situation where you have to decide whether or not it is in your best interest to call to try and make the flush, or fold and save your money.

This is a prime example of where you are going to take advantage of 'pot odds' to work out whether or not it is worth making the call.

What are pot odds? What about flushes and straights?

Basically, just forget about the name if you haven't heard about it before, there's no need to let it throw you off. Just think of 'pot odds' as the method for finding out whether chasing after a draw (like a flush or straight) is going to be profitable. If you're on your toes, you might have already been able to guess that it is generally better to chase after a draw when the bet is small rather than large, but we'll get to that in a minute...

Pot odds will tell you whether or not to call certain sized bets to try and complete your flush or straight draw.

Why use pot odds?

Because it makes you money, of course.

If you always know whether the best option is to fold or call when you're stuck with a hand like a flush draw, you are going to be saving (and winning) yourself money in the long run. On top of that, pot odds are pretty simple to work out when you get the hang of it, so it will only take a split second to work out if you should call or fold the next time you're in a sticky drawing situation. How nice is that?

How to work out whether or not to call with a flush or straight draw.

Now, this is the meat of the article. But trust me on this one, the 'working-out' part is not as difficult as you might think, so give me a chance to explain it to you before you decide to knock it on the head. So here we go...

Essentially, there are two quick and easy parts to working out pot odds. The first is to work out how likely it is that you will make your flush or straight (or whatever the hell you are chasing after), and the second is to compare the size of the bet that you are facing with the size of the pot. Then we use a little bit of mathematical magic to figure out if we should make the call.

1] Find out how likely it is to complete your draw (e.g. completing a flush draw).

All we have to do for this part is work out how many cards we have not seen, and then figure out how many of these unknown cards could make our draw and how many could not.

We can then put these numbers together to get a pretty useful ratio. So, for example, if we have a diamond flush draw on the flop we can work out...

The maths.

There are 47 cards that we do not know about (52 minus the 2 cards we have and minus the 3 cards on the flop).

• 9 of these unknown cards could complete our flush (13 diamonds in total minus 2 diamonds in our hand and the 2 diamonds on the flop).
• The other 38 cards will not complete our flush (47 unknown cards, minus the helpful 9 cards results in 38 useless ones).
• This gives us a ratio of 38:9, or scaled down... roughly 4:1.

So, at the end of all that nonsense we came out with a ratio of 4:1. This result is a pretty cool ratio, as it tells us that for every 4 times we get a useless card and miss our draw, 1 time will we get a useful card (a diamond) and complete our flush. Now all we need to do is put this figure to good use by comparing it to a similar ratio regarding the size of the bet that we are facing.

After you get your head around working out how many cards will help you and how many won't, the only tricky part is shortening a ratio like 38:9 down to something more manageable like 4:1. However, after you get used to pot odds you will just remember that things like flush draws are around 4:1 odds. To be honest, you won't even need to do this step the majority of the time, because there are very few ratios that you need to remember, so you can pick them off the top of your head and move on to step 2.

Texas Holdem Flush Probability Calculator

2] Compare the size of the bet to the size of the pot.

The title pretty much says it all here. Use your skills from the last step to work out a ratio for the size of the bet in comparison to the size of the pot. Just put the total pot size (our opponent's bet + the original pot) first in the ratio, and the bet size second. Here are a few quick examples for you...

• $20 bet into a $100 pot = 120:20 = 6:1
• $0.25 bet creating a total pot size of $1 = 1:0.25 = 4:1
• $40 bet creating a total pot size of $100 = 100:40 = 2.5:1

That should be enough to give you an idea of how to do the second step. In the interest of this example, I am going to say that our opponent (with a $200 stack) has bet $20 in to a $80 pot, giving us odds of 5:1 ($100:$20). This is going to come in very handy in the next step.

This odds calculation step is very simple, and the only tricky part is getting the big ratios down into more manageable ones. However, this gets a lot easier after a bit of practice, so there's no need to give up just yet if you're not fluent when it comes to working with ratios after the first 5 seconds. Give yourself a chance!

To speed up your pot odds calculations during play, try using the handy (and free) SPOC program.

3] Compare these two ratios.

Now then, we know how likely it is that we are going to complete our draw, and we have worked out our odds from the pot (pot odds, get it? It's just like magic I know.). All we have to do now is put these two ratios side to side and compare them...

• 5:1 pot odds
• 4:1 odds of completing our draw on the next card

The pot odds in this case are bigger than the odds of completing our draw, which means that we will be making more money in the long run for every time we hit according to these odds. Therefore we should CALL because we will win enough to make up for the times that we miss and lose our money.

If that doesn't make total sense, then just stick to these hard and fast rules if it makes things easier:

If your pot odds are bigger than your chances of hitting - CALL
If your pot odds are smaller than your chances of hitting - FOLD

So just think of bigger being better when it comes to pot odds. Furthermore, if you can remember back to the start of the article when we had the idea that calling smaller bets is better, you will be able to work out that small bets give you bigger pot odds - makes sense right? It really comes together quite beautifully after you get your head around it.

What if there are two cards to come?

In this article I have shown you how to work out pot odds for the next card only. However, when you are on the flop there are actually 2 cards to come, so shouldn't you work out the odds for improving to make the best hand over the next 2 cards instead of 1?

No, actually.

Even if there are 2 cards to come (i.e. you're on the flop), you should still only work out the odds of improving your hand for the next card only.

The reason for this is that if you work using odds for improving over two cards, you need to assume that you won't be paying any more money on the turn to see the river. Seeing as you cannot be sure of this (it's quite unlikely in most cases), you should work out your pot odds for the turn and river individually. This will save you from paying more money than you should to complete your draw.

I discuss this important principle in a little more detail on my page about the rule of 2 and 4 for pot odds. It's also one of the mistakes poker players make when using odds.

Note: The only time you use odds for 2 cards to come combined is when your opponent in all-in on the flop. In almost every other case, you take it one card at a time.

Playing flush and straight draws overview.

I really tried hard to keep this article as short as possible, but then again I didn't want to make it vague and hazy so that you had no idea about what was going on. I'm hoping that after your first read-through that you will have a rough idea about how to work out when you should call or fold when on a flush or straight draw, but I am sure that it will take you another look over or two before it really starts to sink in. So I advise that you read over it again at least once.

The best way to get to grips with pot odds is to actually start working them out for yourself and trying them out in an actual game. It is all well and good reading about it and thinking that you know how to use them, but the true knowledge of pot odds comes from getting your hands dirty and putting your mind to work at the poker tables.

It honestly isn't that tough to use pot odds in your game, as it will take less than a session or two before you can use them comfortably during play. So trust me on this one, it is going to be well worth your while to spend a little time learning how to use pot odds, in return for always knowing whether to call or fold when you are on a draw. It will take a load off your mind and put more money in your pocket.

To help you out when it comes to your calculations, take a look at the article on simple pot odds. It should make it all a lot less daunting.

Go back to the sublime Texas Hold'em guide.

Can You Afford Not To Use
Poker Tracker 4?

“I wouldn’t play another session of online poker without it”

Texas Holdem Royal Flush Probability

“I play $25NL, and in under 1 week PT4 had paid for itself”

Texas Holdem Flush Probability Chart

Comments